Efeito Doppler

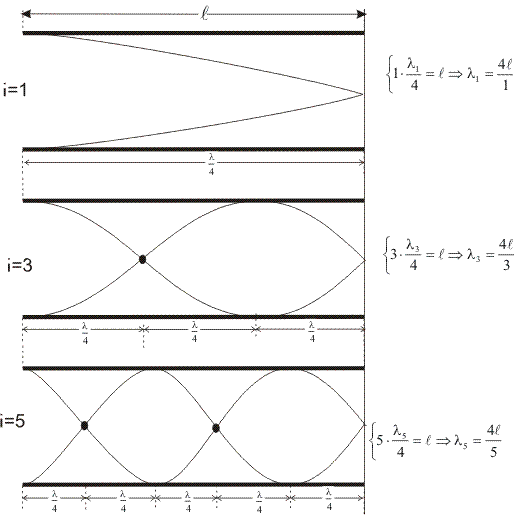
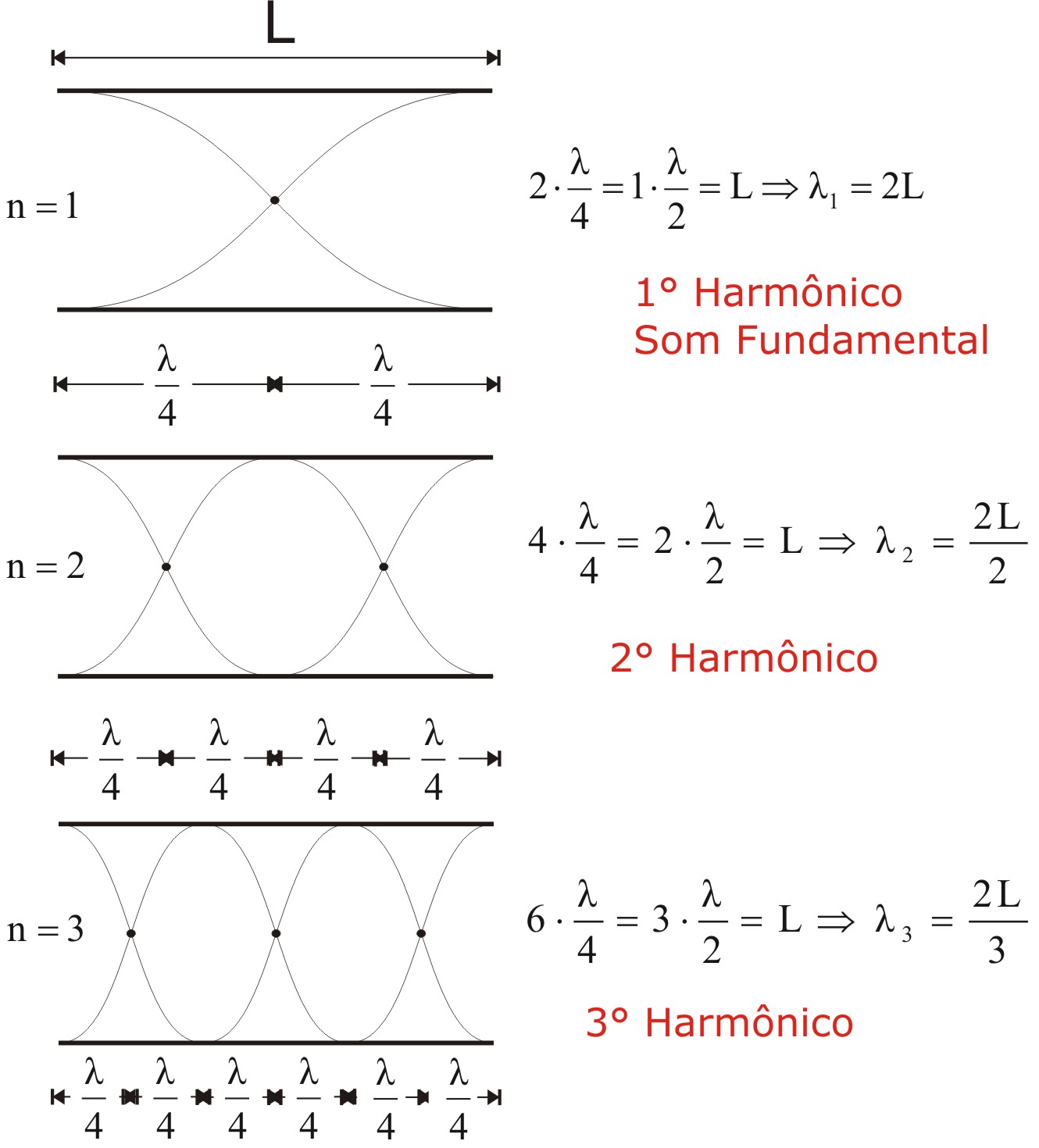
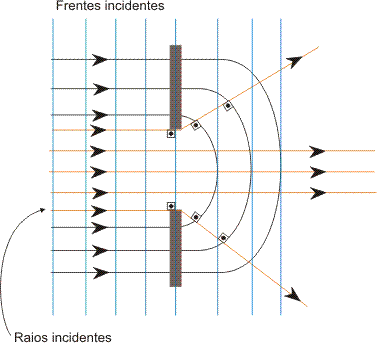
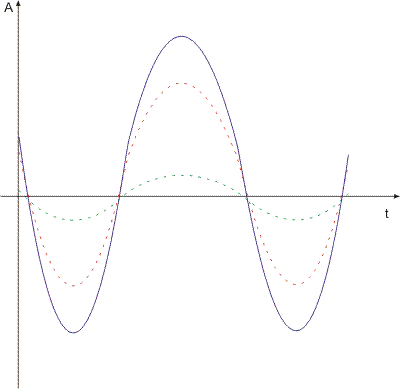
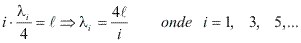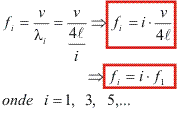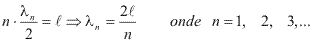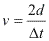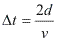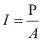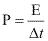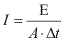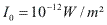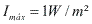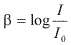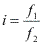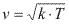Este efeito é descrito como uma característica observada em ondas emitidas ou refletidas por fontes em movimento relativo ao observador. O efeito foi descrito teoricamente pela primeira vez em 1842 por Johann Christian Andreas Doppler, recebendo o nome Efeito Doppler em sua homenagem.

Para ondas sonoras, o efeito Doppler constitui o fenômeno pelo qual um observador percebe freqüências diferentes das emitidas por uma fonte e acontece devido à velocidade relativa entre o a onda sonora e o movimento relativo entre o observador e/ou a fonte.

Considerando:

Podemos determinar uma fórmula geral para calcular a freqüência percebida pelo observador, ou seja, a freqüência aparente.

Supondo que o observador esteja em repouso e a fonte se movimente:

Para o caso onde a fonte se aproxima do observador, há um encurtamento do comprimento da onda, relacionado à velocidade relativa, e a freqüência real será menor que a observada, ou seja:

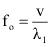
Mas, como a fonte se movimenta, sua velocidade também deve ser considerada, de modo que:

Substituindo 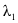 no cálculo da frequência observada:

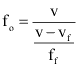
Ou seja:

Para o caso onde a fonte se afasta do observador, há um alongamento aparente do comprimento de onda, nesta situação a dedução do cálculo da frequência observada será análoga ao caso anterior.

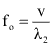
No entanto:

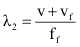
Então:

 

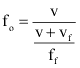
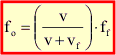
Podemos escrever uma fórmula geral para os casos onde a fonte se desloque e o observador fique parado, se utilizarmos:

Sendo o sinal negativo utilizado no caso onde a fonte se aproxima e positivo no caso em que a fonte se afasta.

 

Busca Geral

 

 

Supondo que  a fonte esteja em repouso e o observador se movimente:

No caso em que o observador se aproxima da fonte, em um mesmo intervalo de tempo ele encontrará mais frentes de onda do que se estivesse parado. Assim a frequência observada deverá ser maior que a frequência emitida pela fonte. Neste caso, o comprimento de onda não é alterado, mas a velocidade de propagação é ligeiramente aumentada.

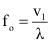
Mas:

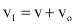 e 

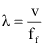
Quando estes dois valores são substituídos no cálculo da frequência observada temos:

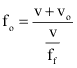
Então:

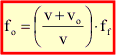
No caso em que o observador se afasta da fonte, em um mesmo intervalo de tempo ele encontrará menor número de frentes de onda do que se estivesse parado. Assim a frequência observada deverá ser menor que a frequência emitida pela fonte. A dedução do cálculo da frequência observada será análoga ao caso anterior, no entanto a velocidade de propagação é ligeiramente reduzida.

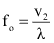
Mas:

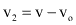 e 

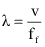
Quando estes dois valores são substituídos no cálculo da frequência observada temos:

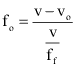
Então:

 

Podemos escrever uma fórmula geral para os casos onde o observador se desloque e a fonte fique parada, se utilizarmos:

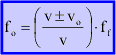
Sendo o sinal negativo utilizado no caso onde a fonte se aproxima e positivo no caso em que a fonte se afasta.

Conhecendo estas quatro possibilidades de alteração na frequência de onda observada podemos escrever uma fórmula geral para o efeito Doppler se combinarmos todos os resultados, sendo ela:

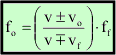
Sendo utilizados os sinais convenientes para cada caso.

Tubos fechados

Considerando um tubo sonoro de comprimento ℓ, cujas ondas se propagam a uma velocidade v.

Assim as possíveis configurações de ondas estacionárias são:

As maneiras de vibrar podem, partindo destes exemplos, ser generalizadas como:

E a frequência dos harmônicos será dada por:

Em um tubo fechado, obtêm-se apenas frequências naturais dos harmônicos ímpares.

Tubos sonoros

Assim como as cordas ou molas, a ar ou gás contido dentro de um tubo pode vibrar com freqüências sonoras, este é o princípio que constitui instrumentos musicais como a flauta, corneta, clarinete, etc. que são construídos basicamente por tubos sonoros.

Nestes instrumentos, uma coluna de ar é posta a vibrar ao soprar-se uma das extremidades do tubo, chamada embocadura, que possui os dispositivos vibrantes apropriados.

Os tubos são classificados como abertos e fechados, sendo os tubos abertos aqueles que têm as duas extremidades abertas (sendo uma delas próxima à embocadura) e os tubos fechados que são os que têm uma extremidade aberta (próxima à embocadura) e outra fechada.

As vibrações das colunas gasosas podem ser estudadas como ondas estacionárias resultantes da interferência do som enviado na embocadura com o som refletido na outra extremidade do tubo.

Em uma extremidade aberta o som reflete-se em fase, formando um ventre (interferência construtiva) e em uma extremidade fechada ocorre reflexão com inversão de fase, formando-se um nó de deslocamento (interferência destrutiva).

 

Tubos abertos

 

Considerando um tubo sonoro de comprimento ℓ, cujas ondas se propagam a uma velocidade v.

Assim as possíveis configurações de ondas estacionárias são:

As maneiras de vibrar podem, partindo destes exemplos, ser generalizadas como:

E a freqüência dos harmônicos será dada por:

Como n não tem restrições, no tubo aberto, obtêm-se freqüências naturais de todos os harmônicos.

Reflexão do som

Assim como para qualquer outra onda, as ondas sonoras, ao atingirem um obstáculo fixo, como uma parede, são refletidas.

A reflexão do som acontece com inversão de fase, mas mantém a mesma velocidade de propagação, mesma freqüência e o mesmo comprimento de onda do som incidente.

Um efeito muito conhecido causado pela reflexão do som é o efeito de eco. Que consiste na reflexão do som que bate em uma parede afastada.

Quando uma pessoa emite um som em direção a um obstáculo, este som é ouvido no momento da emissão, chamado som direto, e no momento em que o som refletido pelo obstáculo retorna a ele.

Sabemos que a velocidade é dada pela distância percorrida pelo som em um determinado tempo, esta distância é dada por duas vezes a distância ao obstáculo refletor, já que o som vai e volta. Assim:

E a velocidade é a de propagação do som no ar.

Ao receber um som, este "permanece" em nós por aproximadamente 0,1s, sendo este intervalo conhecido como persistência acústica.

Pela relação da velocidade:

Se este intervalo de tempo for inferior à persistência acústica (t < 0,1s), o som ouvido após ser refletido parecerá apenas um prolongamento do som direto. A este efeito dá-se o nome dereverberação. Para intervalos maiores que a persistência acústica (t > 0,1s) é instintivo perceber que esta reflexão será ouvida como eco.

Os outros fenômenos acontecem da mesma forma que para as outras ondas estudadas. Tendo uma utilização bastante conhecida a de interferência do som, onde é possível aplicar uma freqüência anti-ruído, a fim de suavizar o som do ambiente.

 

Intensidade sonora

A intensidade do som é a qualidade que nos permite caracterizar se um som é forte ou fraco e depende da energia que a onda sonora transfere.

A intensidade sonora (I) é definida fisicamente como a potência sonora recebida por unidade de área de uma superfície, ou seja:

Mas como a potência pode ser definida pela relação de energia por unidade de tempo:

Então, também podemos expressar a intensidade por:

As unidades mais usadas para a intensidade são J/m² e W/m².

É chamada mínima intensidade física, ou limiar de audibilidade, o menor valor da intensidade sonora ainda audível:

É chamada máxima intensidade física, ou limiar de dor, o maior valor da intensidade sonora suportável pelo ouvido:

Conforme um observador se afasta de uma fonte sonora, aintensidade sonora ou nível sonoro (β) diminui logaritmicamente, sendo representado pela equação:

A unidade utilizada para o nível sonoro é o Bel (B), mas como esta unidade é grande comparada com a maioria dos valores de nível sonoro utilizados no cotidiano, seu múltiplo usual é o decibel (dB), de maneira que 1B=10dB.

Intervalo Acústico

A audição humana é capaz de diferenciar algumas características do som como a sua altura, intervalo e timbre.

A altura do som depende apenas de sua freqüência, sendo definida como a diferenciação entre grave e agudo.

Um tom de maior freqüência é agudo e um de menor é grave.

Os intervalos entre dois sons são dados pelo quociente entre suas frequências. Ou seja:

Como o intervalo é um quociente entre duas medidas de mesma unidade, este não tem dimensão.

Na música é dada uma nomenclatura para cada intervalo:

Intervalo AcústicoRazão de freqüênciaUníssono1:1Oitava2:1Quinta3:2Quarta4:3Terça maior5:4Terça menor6:5Sexta maior5:3Sexta menor8:5Tom maior (M)9:8Tom menor (m)10:9Semitom (s)16:15

As notas musicais de mesmo nome são separadas por um intervalo de uma oitava (2:1)

O timbre de um som é a característica que permite diferenciar dois sons de mesma altura e mesma intensidade, mas que são emitidos por instrumentos diferentes.

Desta forma, uma música executada por um violino e um piano se diferencia pelo timbre.

 

Som e sua propagação

O som é definido como a propagação de uma frente de compressão mecânica ou onda longitudinal, se propagando tridimensionalmente pelo espaço e apenas em meios materiais, como o ar ou a água.

Para que esta propagação ocorra, é necessário que aconteçam compressões e rarefações em propagação do meio. Estas ondas se propagam de forma longitudinal.

Quando passa, a onda sonora não arrasta as partículas de ar, por exemplo, apenas faz com que estas vibrem em torno de sua posição de equilíbrio.

Como as ondas sonoras devem ser periódicas, é válida a relação da velocidade de propagação:

A audição humana considerada normal consegue captar freqüências de onda sonoras que variam entre aproximadamente 20Hz e 20000Hz. São denominadas ondas de infra-som, as ondas que tem freqüência menor que 20Hz, e ultra-som as que possuem freqüência acima de 20000Hz.

De maneira que:

A velocidade do som na água é aproximadamente igual a 1450m/s e no ar, à 20°C é 343m/s.

A propagação do som em meios gasosos depende fortemente da temperatura do gás, é possível inclusive demonstrar experimentalmente que a velocidade do som em gases é dada por:

Onde:

k=constante que depende da natureza do gás;

T=temperatura absoluta do gás (em kelvin).

 

Como exemplo podemos tomar a velocidade de propagação do som no ar à temperatura de 15° (288K), que tem valor 340m/s.

 

Exemplo:

Sabendo que à 15°C o som se propaga à 340m/s, qual será sua velocidade de propagação à 100°C?

Lembrando que:

15° = 288K

100° = 373K

Experiência de Young

Por volta do século XVII, apesar de vários físicos já defenderem a teoria ondulatória da luz, que afirmava que a luz era incidida por ondas, a teoria corpuscular de Newton, que descrevia a luz como um partícula, era muito bem aceita na comunidade científica.

Em 1801, o físico e médico inglês, Thomas Young foi o primeiro a demonstrar, com sólidos resultados experimentais, o fenômeno de interferência luminosa, que tem por consequência a aceitação da teoria ondulatória. Embora, hoje em dia, a teoria aceita é a dualidade onda-partícula, enunciada pelo físico francês Louis-Victor de Broglie, baseado nas conclusões sobre as características dos fótons, de Albert Einstein.

Na experiência realizada por Young, são utilizados três anteparos, sendo o primeiro composto por um orifício, onde ocorre difração da luz incidida, o segundo, com dois orifícios, postos lado a lado, causando novas difrações. No último, são projetadas as manchas causadas pela interferência das ondas resultantes da segunda difração.

Ao substituir-se estes orifícios por fendas muito estreitas, as manchas tornam-se franjas, facilitando a visualização de regiões mais bem iluminadas (máximos) e regiões mal iluminadas (mínimos).

Observa-se que o máximo de maior intensidade acontece no centro, e que após este máximo, existem regiões de menor intensidade de luz, e outras de mínimos, intercalando-se.

 

Difração de ondas

Partindo do Princípio de Huygens, podemos explicar um outro fenômeno ondulatório, a difração.

O fenômeno chamado difração é o encurvamento sofrido pelos raios de onda quando esta encontra obstáculos à propagação.

Imagine a situação em que uma onda se propaga em um meio, até onde encontra uma fenda posta em uma barreira.

Este fenômeno prova que a generalização de que os raios de onda são retilíneos é errada, já que a parte que atinge a barreira é refletida, enquanto os raios que atingem a fenda passam por ela, mas nem todas continuam retas.

Se esta propagação acontecesse em linha reta, os raios continuariam retos, e a propagação depois da fenda seria uma faixa delimitada pela largura da fenda. No entanto, há um desvio nas bordas.

Este desvio é proporcional ao tamanho da fenda. Para o caso onde esta largura é muito inferior ao comprimento de onda, as ondas difratadas serão aproximadamente circulares, independente da forma geométrica das ondas incidentes.

Princípo de Huygens

Christian Huygens (1629-1695), no final do século XVII, propôs um método de representação de frentes de onda, onde cada ponto de uma frente de onda se comporta como uma nova fonte de ondas elementares, que se propagam para além da região já atingida pela onda original e com a mesma freqüência que ela. Sendo esta idéia conhecida como Princípio de Huygens.

Para um considerado instante, cada ponto da frente de onda comporta-se como fonte das ondas elementares de Huygens.

A partir deste princípio, é possível concluir que, em um meio homogêneo e com as mesmas características físicas em toda sua extensão, a frente de onda se desloca mantendo sua forma, desde que não haja obstáculos.

Desta forma:

Ressonância

É o fenômeno que acontece quando um sistema físico recebe energia por meio de excitações de freqüência igual a uma de suas freqüências naturais de vibração. Assim, o sistema físico passa a vibrar com amplitudes cada vez maiores.

Cada sistema físico capaz de vibrar possui uma ou mais frequências naturais, isto é, que são características do sistema, mais precisamente da maneira como este é construído. Como por exemplo, um pêndulo ao ser afastado do ponto de equilíbrio, cordas de um violão ou uma ponte para a passagem de pedestres sobre uma rodovia movimentada.

Todos estes sistemas possuem sua frequência natural, que lhes é característica. Quando ocorrem excitações periódicas sobre o sistema, como quando o vento sopra com freqüência constante sobre uma ponte durante uma tempestade, acontece um fenômeno de superposição de ondas que alteram a energia do sistema, modificando sua amplitude.

Conforme estudamos anteriormente, se a freqüência natural de oscilação do sistema e as excitações constantes sobre ele estiverem sob a mesma frequência, a energia do sistema será aumentada, fazendo com que vibre com amplitudes cada vez maiores.

Um caso muito famoso deste fenômeno foi o rompimento da ponte Tacoma Narrows, nos Estados Unidos, em 7 de novembro de 1940. Em um determinado momento o vento começou soprar com freqüência igual à natural de oscilação da ponte, fazendo com que esta começasse a aumentar a amplitude de suas vibrações até que sua estrutura não pudesse mais suportar, fazendo com que sua estrutura rompesse.

O caso da ponte Tacoma Narrows pode ser considerado uma falha humana, já que o vento que soprava no dia 7 de Novembro de 1940 tinha uma frequência característica da região onde a ponte foi construída, logo os engenheiros responsáveis por sua construção falharam na análise das características naturais da região. Por isto, atualmente é feita uma análise profunda de todas as possíveis características que possam requerer uma alteração em uma construção civil.

Imagine que esta é uma ponte construída no estilo pênsil, e que sua frequência de oscilação natural é dada por:

Ao ser excitada periodicamente, por um vento de freqüência:

A amplitude de oscilação da ponte passará a ser dada pela superposição das duas ondas:

Se a ponte não tiver uma resistência que suporte a amplitude do movimento, esta sofrerá danos podendo até ser destruída como a ponte Tacoma Narrows.